�quation de Schr�dinger
Nous avons vu qu'� chaque particule l'on peut associer une onde. L'amplitude de l'onde associ�e � un �lectron est d�termin�e par une fonction math�matique : la fonction d'onde ou orbitale :
Cette fonction se note par la lettre grecque psy : 
La fonction d'onde n'a pas de r�alit� "physique",
elle ne repr�sente rien d'un point de vue physique, par contre 
repr�sente la densit� �lectronique en un point (nombre d'e-/nm�)
et permet d'�valuer la probabilit� de trouver un �lectron � cet endroit.
Si l'on calcule sur l'ensemble de l'espace :
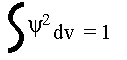
voir le d�tail de l'�quation de Schr�dinger
L'atome n'a donc pas de limite physique pr�cise dans l'espace. Pour trouver les fonctions d'ondes, il faut r�soudre l'�quation de schr�dinger.
L'�quation et son origine
|
Copyright (c) 2000 - 2020 | Miseur Ludovic | www.lachimie.net | tous droits r�serv�s | remis � jour le : 21/10/2020 |
|
|
|
Comment citer cette page : |
| Miseur, L. (2020). Lachimie.net - Equation de Schroedinger. La Chimie.net. http://www.lachimie.net | |
